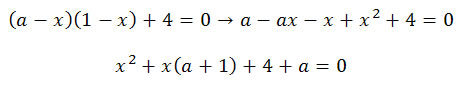1) Escreva a matriz A = (aij) do tipo 3x4 sabendo que aij = 2i – 3j.
2) Dada a matriz , calcule a11 + a21 – a13 + 2a22.
3) Dada a matriz C = , calcule 3a31 – 5a42.
4) Uma loja vende sapatos femininos de três marcas X; Y; Z e tamanhos de
Tamanho 35 | 30 pares |
Tamanho 36 | 50 pares |
Tamanho 37 | 25 pares |
Tamanho 38 | 18 pares |
Tamanho 39 | 10 pares |
Tamanho 40 | 7 pares |
Analogamente, a loja possui, das marcas Y e Z, sapatos femininos assim distribuídos:
Tamanho | 35 | 36 | 37 | 38 | 39 | 40 |
Quantidade da marca Y | 8 | 7 | 9 | 28 | 10 | 8 |
Quantidade da marca Z | 0 | 10 | 15 | 12 | 9 | 3 |
a) Escreva sob forma de matriz todas as informações dadas.
b) Quantos pares de sapato ela tem do tamanho que você usa?
c) Qual é o tamanho que possui mais pares em estoque?
d) Escreva em linguagem coloquial o significado dos elementos a35 e a22 da matriz do item a.
5) Escreva a matriz A = (aij) do tipo 3x4 sabendo que:
aij = 2i – 3j se i = j e aij = 3i – 2j se i ¹ j.
6) Escreva a matriz coluna do tipo 7x1 tal que aij = 2i + 3j.
7) a) Escreva a matriz linha do tipo 1x7 tal que aij = 2i + 3j.
b) Escreva a matriz linha do tipo 1x7 tal que aij = 3i + 2j.
8) a) Determine a matriz A do tipo 3x2 sabendo que aij = (2i -3j)/2.
b) De que tipo é a matriz At da matriz do item a?
c) Determine a matriz At da matriz A do item a?
9) Dadas as matrizes e
Determine x e y de modo que a matriz A seja igual à matriz B.
10) Calcule o valor de x para que sejam iguais as duas matrizes e
.
11) Calcule o valor de x, y e z de modo que as matrizes e
sejam iguais.
12) Sendo ,
e
Resolva as equações matriciais abaixo, determinando o valor da matriz X.
a) X + A = 2B – C.
b) X – C = 2A + 3B.
c) X + 2B = 3A – C.
13) Sendo e
a) Calcule AB b) Calcule BA c) Calcule A2 d) Calcule B2
14) Calcule x; y e z em cada um dos produtos de matrizes dados:
a) b)
15) Seja dada a equação matricial: .
a) Identifique o tipo da matriz X.
b) Determine a matriz X.
16) Determine o produto da matriz pela matriz transposta em cada um dos itens abaixo.
a) b)
17) Determine as inversas das matrizes:
a) b)
c)
d)
18) Dadas as matrizes: e
determine a matriz X tal que X = A-1.B.

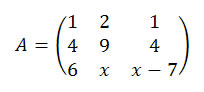
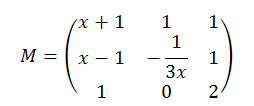
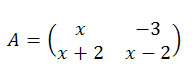
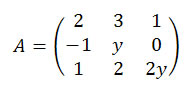
.jpg)
.jpg)