LISTA DE EXERCÍCIOS - LOGARITMOS

LISTA DE EXERCICIOS - PROGRESSÃO GEOMÉTRICA - 1° ANO

1 - A sequência seguinte é uma progressão geométrica, observe: (2, 6, 18, 54...). Determine o 8º termo dessa progressão.

 

2 - (Vunesp – SP – Adaptado) Várias tábuas iguais estão em uma madeireira. Elas deverão ser empilhadas respeitando a seguinte ordem: uma tábua na primeira vez e, em cada uma das vezes seguintes, tantas quantas já estejam na pilha. Por exemplo:

Determine a quantidade de tábuas empilhadas na 12ª pilha.

 

3 - Sabendo que uma PG tem a1 = 4 e razão q = 2, determine a soma dos 10 primeiros termos dessa progressão.

 

4 - Calcule o oitavo termo da PG (3, 6, 12, …)

 

5 - Calcule a razão de uma PG, sabendo que a5=64 e a1=4 e escreva a PG.

 

6 - Determine o número de termos de uma PG, onde,

 

7 - Sendo x - 3, x ,x + 6 três termos consecutivos de uma PG, calcule o valor de x e escreva a PG.

 

8 - PUC/RJ – 2017 - Os termos da soma S = 4 + 8 + 16 + ... + 2048 estão em progressão geométrica. Determine a soma desses termos.

 

9 -  Dada a PG (2, 4, 8,... ), calcule o seu décimo termo.

 

10 - Considere que x − 4 , 2x + 4  e 10x - 4 são termos consecutivos de uma PG. Calcule x de modo que eles sejam positivos.

 

11 - Determine x de modo que a sucessão (x – 1 , x + 2 , 3x )seja uma PG crescente.

 

12 - A sequência (4x, 2x + 1, x – 1) é uma PG. Então, o valor de x é

 

 

13 - O número de termos da PG (1/9 ; 1/3; 1; … ;729) é?

 

14 - Determine o 12ª elemento de uma progressão geométrica onde o primeiro elemento é 1 e a razão é 2.

 

15 - Determine o primeiro elemento de uma P.G. com 6 elementos onde a razão é 3 e o último termo 1 701.

 

16 - Determine o primeiro elemento de uma P.G. com 8 elementos onde o último termo é 512 e a razão é 2.

 

17 - Sobre as propriedades estudadas de P.G julgue os itens abaixo em CORRETO ou ERRADO:

I - Numa P.G tem-se que a1 = 3 e a8 = 384, então sua razão é 2.

II - O 8º termo da P.G (1,2,4 ...) é 128.

III - O número de termos da P.G (4,8,16, ...,1024) é 10.

Quantos itens são CORRETOS:

a) 1                       b) 2               c) 3              d) 0

 

18 - Uma seqüência é uma progressão geométrica se cada termo, a partir do segundo, é igual ao produto do termo anterior por uma constante q (q diferente de zero) chamada razão da P.G.. Uma das propriedades da P.G. é: se três termos de uma P.G. são consecutivos, então o quadrado do termo do meio é sempre igual ao produto dos 2 outros dois. Sendo assim, calcule o valor de x na P.G. (x - 3, x, x + 6) e assinale a alternativa correta:

a) x = 4               b) x = 2                 c) x = 6           d) x = 5

 

19 - Em uma P.G. de razão 3, o 7º, termo é 1458. Calcule a1.

 

20 -  Calcule o número de termos das seguintes P.G.

a) (4, 8, 16,…,1024)

 

b) (9, 3, 1,…,1/81)

 

21 - Interpole quatro meios geométricos entre 2 e 486.

 

22 - Insira três meios geométricos positivos entre 1/27 e 3.

 

23 - Calcule a soma dos 10 primeiros termos da P.G. (2, 4, 8, 16,…)

 

24 - Determine a soma dos 5 primeiros termos da P.G. (2, -6, 18,…)

 

25 - Determinar o décimo termo da PG (1, 2, 4, 8, 16, …)

LISTA DE EXERCÍCIOS - FUNÇÃO DO 1° GRAU - 1° ANO - ENSINO MÉDIO

1) Dados os conjuntos A = { 5,6,7,8,9,10} e o conjunto B = { 10,20,27,32,37,42,47,50} e a função h: A -> B definida pela lei de formação h(x) = 3x – 3. Diante desses dados, encontre o conjunto Im (h).

2) Dados o conjunto C = {-1,0,2} e o D = {0,1,2,3,4} e a função g: C-> D definida pela lei de formação g(x) = x + 2. Diante desses dados, encontre o conjunto Im (g).

3) Sejam A = { -1,1,3,5} e B = {0,1,2,3,4,5,6}. Para a função f: A-> B, definida por f(x) = x+1, determine:

a) Conjunto dos pares ordenados de f;
b) Diagrama de f;
c) Domínio de f;
d) Contradomínio de f;
e) Conjunto imagem de f.

4) Um função associa a cada número a sua quarta parte. Se o conjunto imagem dessa função é Im f = { 0,1/2, 3}, qual é o domínio da função f?

5) Uma função associa a cada elemento do seu domínio o triplo dele. Se o conjunto imagem dessa função é Im g = {3,6,12}, qual é o domínio da função g?

6)Dada a função do 1º grau f(x) = 1 – 5x, determine:

a) f(0)
b) f(-1)
c) f(1/5)
d) f(-1/5)
e) f(8)
f) f(10)
g) f(12)

7) Considere a função do 1º grau f(x) = - 3x + 2. Determine os valores de x para que se tenha:

a) f(x) = 0
b) f(x) = 11
c) f(x) = - ½
d) f(x) = 2
e) f(x) = - 7
f) f(x) = 1
g) f(x) = - 1
h) f(x) = - 10

8)Verifique se a equação f(x) = 2x+ 1, determina ou não uma função de A em B, dados A = {1,3,5} e B = { 3,4,5}

9) Verifique se a equação g(a) = 2a + 5, determina ou não uma função de X em Y, dados X = {2,4,6,8} e Y = { 9,10,13,15,17,19,21}

10) Dada a função f(x) = ax + 2, determine o valor de a para que se tenha f(4) = 22.

11) Dada a função g(x) = ax + b e sabendo-se que g(3) = 5 e g(-2) = - 5. Calcule g(1/2). 

12) Em algumas cidades, você pode alugar um carro por 154 reais por dia mais um adicional de 16 reais por km rodado. Diante dessa situação:

a) Determine a função por um dia de aluguel do carro.
b) Calcule o preço para se alugar por um dia e dirigi-lo por 200 km.

13) O preço a ser pago por uma corrida de táxi inclui uma parcela fixa, denominada bandeirada, e uma parcela que depende da distância percorrida. Se a bandeirada custa R$ 5,50 e cada quilômetro rodado custa R$ 0,90, calcule:

a) O preço de uma corrida de 10 km.
b) A distância percorrida por um passageiro que pagou R$ 19,00 pela corrida.

14) O preço a ser pago por uma corrida de táxi inclui uma parcela fixa, denominada bandeirada, e uma parcela que depende da distância percorrida. Se a bandeirada custa R$ 3,44 e cada quilômetro rodado custa R$ 0,86, calcule:

c) O preço de uma corrida de 11 km.
d) A distância percorrida por um passageiro que pagou R$ 21,50 pela corrida.

15) Na revelação de um filme, uma óptica calcula o preço a ser cobrado usando a fórmula P = 12 + 0,65n, onde P é o preço, em reais, a ser cobrado e n o número de fotos reveladas do filme.

a) Quanto pagarei se forem reveladas 22 fotos do meu filme?
b) Se paguei a quantia de R$ 33,45 pela revelação, qual o total de fotos reveladas?

16) Dada a função f (x) = 8x + 15, calcule:

a) f(0) – f(3)
b) f(5) – f (10)
c) f(7) + f(-3)
d) f(2) + f( 3)

17) Dada a função f(x) = 3x + 1, calcule:

a) f(9) – f(1)
b) f(4) – f(-2)
c) f(-5) + f(3)
d) f(2) + f(6)
e) f(10) + f (3)

AVALIAÇÃO BIMESTRAL - 1º BIMESTRE - 1º ANO - ENSINO MÉDIO- 2023

1  - Numa classe de 30 alunos, 16 gostam de matemática e 20 de história. O número de alunos desta classe que gostam de matemática e de história é:

a) Exatamente 16
b) Exatamente 10
c) No máximo 8

d) No mínimo 6 
e) Exatamente 18

2 - Numa universidade são lidos apenas 2 jornais X e Y. 80% dos alunos da mesma lêem o jornal X e 60 % lêem o jornal Y. Sabendo-se que todo aluno é leitor de pelo menos um dos jornais, assinale a alternativa que corresponde ao percentual de alunos que lêem ambos.

a) 80%
b) 14 %
c) 40% 
d) 60%

e) 48% 

3 - (UNB-Adaptada) De 200 pessoas que foram pesquisadas sobre suas preferências em assistir aos campeonatos de corrida pela televisão, foram colhidos os seguintes dados: 

55 dos entrevistados não assistem; 

101 assistem às corridas de Fórmula l; 

27 assistem às corridas de Fórmula l e de Motovelocidade; 

Quantas das pessoas entrevistadas assistem, exclusivamente, às corridas de Motovelocidade?

a) 36 pessoas

b) 74 pessoas

c) 44 pessoas

d) 71 pessoas

e) 47 pessoas

4 - Observe os conjuntos a seguir e marque a alternativa correta.

5 - Represente os conjuntos A = {- 3, - 1, 0, 1, 6, 7} , B = {- 4, 1, 3, 5, 6, 7} e C = {- 5, - 3, 1, 2, 3, 5} no diagrama de Venn e em seguida determine:

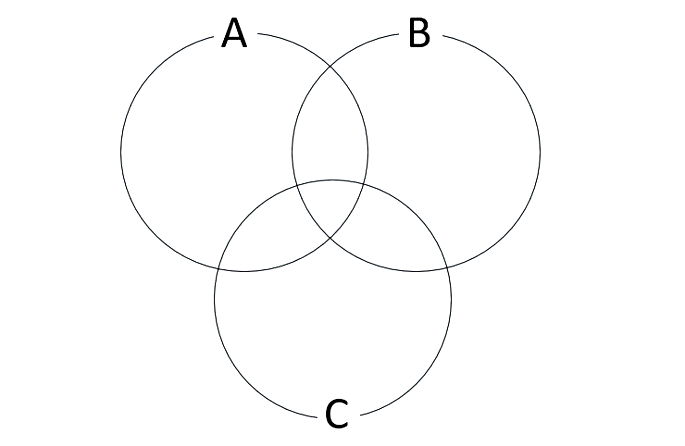
6 - (UEL-PR) Num dado momento, três canais de TV tinham, em sua programação, novelas em seus horários nobres: a novela A no canal A, a novela B no canal B e a novela C no canal C. Numa pesquisa com 3000 pessoas, perguntou-se quais novelas agradavam. A tabela a seguir indica o número de telespectadores que designaram as novelas como agradáveis.

Novelas	Número de telespectadores
A	1450
B	1150
C	900
A e B	350
A e C	400
B e C	300
A, B e C	100

Quantos telespectadores entrevistados não acham agradável nenhuma das três novelas?

a) 300 telespectadores.
b) 370 telespectadores.
c) 450 telespectadores.
d) 470 telespectadores.
e) 500 telespectadores.

7 - Considere os conjuntos

A = {1, 4, 7}
B = {1, 3, 4, 5, 7, 8}

É correto afirmar que:

GABARITO

1 - D

2 - C

3 - C

4 - D

5 - a) {1, 6, 7}; b) {-5, -4, -3, 1, 2, 3, 5, 6, 7}; c) {-5, 2, 3, 5} e d) {1, 3, 5, 6, 7}.

6 - C

7 - B

LISTA DE EXERCÍCIOS - FUNÇÃO HORÁRIA DO ESPAÇO - 1º ANO - ENSINO MÉDIO - FÍSICA - 2023

1 -  (Mackenzie-SP) Uma partícula descreve um movimento uniforme. A função horária dos espaços, com unidades do Sistema Internacional de Unidades é:  s = -2,0 + 5,0.t.  Nesse caso, podemos afirmar que a velocidade escalar da partícula é:

a) -2 m/s e o movimento é retrógrado.

b)  -2 m/s e o movimento é progressivo.

c) 5,0 m/s e o movimento é progressivo

d) 5,0 m/s e o movimento é retrógrado

e) -2,5 m/s e o movimento é retrógrado

2 - Sabendo que o espaço do móvel varia com o tempo, e obedece a seguinte função horária do espaço: S = -100 + 25 . t, determine:

a) o espaço no instante 8s.

b) o instante quando o móvel passa na origem das posições.

c) Informe se o movimento do móvel é progressivo ou retrógrado.

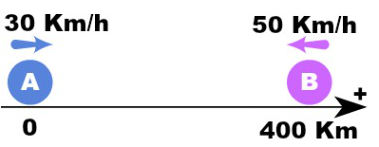
3 - Determine o tempo necessário para que os móveis da figura a seguir se encontrem.

a) 2h

b) 3h

c) 4h

d) 5h

e) 6h

4 - A partir do gráfico abaixo, escreva a função horária da posição para o móvel que executa movimento uniforme.

a) S = 50 + 5.t

b) S = 50 + 15.t

c) S = 50 – 5.t

d) S = 50 + 10.t

e) S = 50 – 8.t

5 - Um móvel com velocidade constante igual a 20 m/s parte da posição 5 m de uma reta numerada e anda de acordo com o sentido positivo da reta. Determine a posição do móvel após 15 s de movimento.

a) 105 m

b) 205 m

c) 305 m

d) 405 m

e) 505 m

6 - Um homem sai da posição 15 m de uma pista de caminhada e anda até a posição 875 m mantendo uma velocidade constante de 2 m/s. Sabendo disso, determine o tempo gasto para completar a caminhada.

a) 430 s

b) 320 s

c) 450 s

d) 630 s

e) 530 s

7 -  (UTP) Numa determinada trajetória, um ponto material tem função horária: x = 10 – 2t (tempo em segundos e posição em metros). No instante t = 3 s, a posição do ponto será:

a) 6 m
b) 10 m
c) 4 m
d) 16 m
e) n.d.a.

8 -  (EESJC-SP) Uma partícula tem equação horária dos espaços dada por:

s = 100 – 20t (SI)

a) Qual a trajetória da partícula?
b) Em que instante a partícula passa pela origem dos espaços?

9 - (UNITAU-SP) Um automóvel percorre uma estrada com função horária V = – 40 + 80t, onde v é dado em km e t em horas. O automóvel passa pelo km zero após:

a) 1,0 h
b) 1,5 h
c) 0,5 h
d) 2,0 h
e) 2,5 h

10 - Um móvel descreve um movimento de acordo com a função horária do espaço:

s = – 40 + 20t (SI)

Determine o instante que esse móvel passa pelo espaço s = 60 m.

11 - Um móvel descreve um movimento de acordo com a função horária do espaço:

                                                              s = 10 + 2t (SI)

Determine o instante que esse móvel passa pelo espaço s = 30 m.

12 - O movimento de um móvel respeita a função horária do espaço:

s = – 100 + 5t (SI)

Qual o instante em que esse móvel passa pelo espaço s = – 50 m.

13 - Determine o instante em que um automóvel que descreve um movimento sobre uma rodovia descrito pela função horária do espaço abaixo, passa pelo marco km 500?

s = 50 + 90t (s em km e t em horas)

14 - Dadas as funções horárias a seguir, determine a posição inicial e a velocidade escalar (no SI) e classifique o movimento em progressivo ou retrógrado.

a) s = 4t
b) s = -3t
c) s = 5 + 2t
d) s = 10 – 4t
e) s = -7 + 3t
f) s = -8 – 5t

15 - A equação horária S = 3 + 4 . t, em unidades do sistema internacional, traduz, em um dado referencial, o movimento de uma partícula, determine:

a) Para o instante t = 3 s qual sua  posição da partícula.

b) a velocidade da partícula.

16 - Um automóvel percorre uma estrada com função horária S= -40 + 80t, onde x é dado em km e t em horas. O automóvel passa pelo km zero após:

a) 1,0 h
b) 1,5 h
c) 0,5 h
d) 2,0 h
e) 2,5 h

17 - Uma partícula tem equação horária dos espaços dada por:

S = 100 – 20t (SΙ)

a) Qual a trajetória da partícula?
b) Em que instante a partícula passa pela origem dos espaços?

GABARITO:

1 - LETRA C

Resolvendo...
A forma mais fácil de identificar a resposta certa é comparando a equação e os valores dados.
x = xo + v .t
x = -2,0 + 5,0.t 

2 - a) x = -100 +25 .8

    x = -100 +200
    x = 100m

b) Temos que calcular o tempo quando o espaço final for 0
x = -100 + 25.t
0 = -100 +25.t
100 = 25t
100÷25 = t
4 = t
Logo, t = 4s

c) O movimento é progressivo, pois a velocidade é positiva (+25m/s)

3 - LETRA “D”

Escrevendo a função horária da posição do movimento uniforme para os corpos A e B, temos:

S_A = S₀ + v.t → S_A = 0 + 30.t → S_A = 30.t

S_B = S₀ – v.t → S_B = 400 – 50.t

Sabendo que no momento do encontro S_A = S_B, temos:

S_A = S_B

30.t = 400 – 50.t

50.t + 30.t = 400

80.t = 400

t = 400
    80

t = 5 h

4 - LETRA “C”

Analisando o gráfico, temos:

• Posição inicial: S₀ = 50 m;

• Tempo até atingir a posição 0: t = 10 s;

• Tipo de movimento: Reta decrescente indica movimento retrógrado, logo, a velocidade é negativa.

A partir da definição de velocidade média, podemos determinar a velocidade do móvel:

v = Δs
     Δt

v = (0 – 50)
     10

v = - 5m/s

De posse da velocidade, podemos determinar a função horária da posição para esse móvel.

S = S₀ + v.t

S = 50 – 5.t

5 - LETRA “C”

A partir dos dados fornecidos, temos:

v = 20 m/s

S₀ = 5m

t = 15s

A partir da função horária da posição para o movimento uniforme, temos:

S = S₀ + v.t

S = 5 + 20.15

S = 5 + 300

S = 305 m

6 - LETRA “A”

Do enunciado da questão, temos:

S₀ = 15 m

S = 875 m

v = 2 m/s

A partir da função horária da posição para o movimento uniforme, podemos escrever que:

S = S₀ + v.t

875 = 15 + 2.t

875 – 15 = 2.t

2.t = 860

t = 430 s

7 - LETRA - C

a) Como x = 10 – 2t, temos no tempo t = 3s:
x = 10 – 2∗3
x = 10 – 6
x = 4 m

8 - 

a) Somente com a função horária do espaço, não podemos dizer a respeito da trajetória.
b) s = 0 (origem dos espaços)
s = 100 – 20t
0 = 100 – 20t
20t = 100
t = 100/20
t = 5s

9 -  LETRA C

– Pelo quilômetro zero é quando x = 0, temos:
0 = – 40 + 80t
40 = 80t
80t = 40
t = 40/80
t = 0,5 h

10 - No espaço s = 60 m , temos:
60 = – 40 + 20t
60 + 40 = 20t
100 = 20t
20t = 100
t = 100/20
t = 5 s

11 -  No espaço s = 30 m , temos:
30 = 10 + 2t
30 – 10 = 2t
20 = 2t
2t = 20
t = 20/2
t = 10 s

12 -  No espaço s = – 50 m , temos:
– 50 = – 100 + 5t
– 50 + 100 = 5t
50 = 5t
5t = 50
t = 50/5
t = 10 s

13 -  No km 500 , temos:
500 = 50 + 90t
500 – 50 = 90t
450 = 90t
90t = 450
t = 450/90
t = 5 h

LISTA DE EXERCÍCIOS - VELOCIDADE MÉDIA - 1º ANO - ENSINO MÉDIO - FÍSICA - 2023

1 – Qual o valor da velocidade escalar média, em m/s, de um móvel que se desloca 432 km em 6 h? 

2 – Qual o valor da velocidade escalar média, em m/s, de um móvel que parte de uma cidade e 3 h depois está numa cidade distante 324 km? 

3 – Se um móvel parte de um ponto às 2 h e às 6 h está num ponto distante 300 km, qual a sua velocidade escalar média, em km/h? 

4 – Se um móvel parte de um ponto na estrada marcado como 20 km às 2 h e às 5 h está num ponto marcado com 320 km. Qual a sua velocidade escalar média neste trecho? 

5 – Um móvel percorre 200 km em 3h e depois percorre mais 300 km em 5h. Qual a sua velocidade escalar média na viagem completa? 

6 – Um móvel viaja 200 km a uma velocidade escalar média constante de 80 km/h. Em quanto tempo ele percorreu esta distância? 

7 – Um móvel viaja uma distância a uma velocidade escalar média constante de 80 km/h durante 5 h. Qual essa distância?

8) Um atleta que se preparou para participar das olimpíadas de Atlanta corre a prova dos 100m em apenas 9,6s. Calcule a velocidade média. 

9) Qual a velocidade média de um atleta que faz 50m em 4 s? 

10) Considere um corpo viajando a 40Km/h. Nessa velocidade, qual a distância percorrida pelo móvel em 15 minutos? 

11) Um carro fez uma viagem a partir do Km 120 de uma rodovia até o Km 30. 

a) Qual o deslocamento do carro? 

b) Qual a posição final e inicial? 

c) Qual a velocidade média do carro, quando se passaram 2h? 

12) Um carro percorre uma rodovia passando pelo Km 20 às 9h e pelo Km 45 às 10h. 

a) Quais as posições nos instantes dados? 

b) Qual o deslocamento? 

c) Qual a velocidade média? 

13) A velocidade média de um carro é de 72Km/h. Em quanto tempo ele anda 100m? 

14) Um carro parte do km 12 de uma rodovia e desloca-se sempre no mesmo sentido até o km 90. Determine o deslocamento do carro.

15) Um automóvel deslocou-se do km 20 até o km 65 de uma rodovia, sempre no mesmo sentido. Determine o deslocamento do automóvel. 

16) Quando o brasileiro Joaquim Cruz ganhou a medalha de ouro nas Olimpíadas de Los Angeles, correu 800m em 100s. Qual foi sua velocidade média? 

17) Suponha que um carro gaste 3 horas para percorrer a distância de 45 km. Qual a velocidade média deste carro em Km/h e m/s? 

18) Se um carro demorou 40 segundos para percorrer uma distância de 800 metros, qual foi a velocidade média deste carro? 

19) João demorou 30 minutos para percorrer uma distância equivalente a 5 km. Qual foi a velocidade média de João? 

20) Qual será a distância percorrida por um veículo que mantém uma velocidade média de 80 km/h durante 3 horas? 

21) Um ciclista faz um determinado percurso em 3 horas, registrando uma velocidade média de 15 km/h. Se fizesse o mesmo percurso a uma velocidade média de 9 km/h, quanto tempo gastaria a mais?

22) (Cesgranrio). Um automóvel passou pelo marco 24 km de uma estrada às 12 horas e 7 minutos. A seguir, passou pelo marco 28 km da mesma estrada às 12 horas e 11 minutos. Qual foi a velocidade média do automóvel, entre as passagens pelos dois marcos, foi de aproximadamente? 

23) (Fuvest) Após chover na cidade de São Paulo, as águas da chuva descerão o rio Tietê até o rio Paraná, percorrendo cerca de 1.000km. Sendo de 4km/h a velocidade média das águas, o percurso mencionado será cumprido pelas águas da chuva em aproximadamente: 

24) Um móvel percorre uma distância de 80 m em 5 segundos .Qual sua velocidade média? 

25) Um carro faz uma viagem de 180 km em 2h. Qual sua velocidade média? 

26) Um automóvel, num intervalo de tempo de 2 h, passa do marco quilométrico 140 km de uma estrada para o marco quilométrico 200 km da mesma estrada. Qual a velocidade média desse automóvel nesse tempo? 

27) . Qual o deslocamento de um carro que viaja com velocidade escalar média de 80 km/h, durante 1h15min?

28) Qual o deslocamento de um carro que viaja com velocidade escalar média de 80 km/h, durante 1h15min? 

29) Se uma viagem de 330 km é feita com velocidade média de 90 km/h, quanto tempo será gasto? 

30) Às 8h32min10s, um caminhão se encontra no marco quilométrico 50 km de uma estrada. Às 10h14min20s, o caminhão se encontra no marco quilométrico 210 km da mesma estrada. Determine a velocidade média do caminhão. 

31) Um avião vai de S. Paulo a Recife em 1h40min. A distância entre essas duas cidades é de aproximadamente 3000 km. Qual a velocidade média desse avião? 

32) O velocímetro de um carro indica 72 km/h. Expresse a velocidade deste carro em m/s. 

33) Uma velocidade de 36 km/h corresponde a quantos metros por segundo? E 15 m/s correspondem a quantos quilômetros por hora? 

34) A velocidade escalar média de um certo ponto material, num dado intervalo de tempo, é de 180Km/h. Exprima essa velocidade em m/s.

35) Um nadador percorre uma piscina de 50m de comprimento em 25s. Determine a velocidade média desse nadador. 

36) Suponha que um carro gaste 4 horas para percorrer a distância de 400km. Qual a velocidade média deste carro? 

37) Um automóvel passou pelo marco 30km de uma estrada às 12 horas. A seguir, passou pelo marco 150km da mesma estrada às 14 horas. Qual a velocidade média desse automóvel entre as passagens pelos dois marcos? 

38) No verão brasileiro, andorinhas migram do hemisfério norte para o hemisfério sul numa velocidade média de 25km/h. Se elas voam 12horas por dia, qual a distância percorrida por elas num dia? 

39) Uma pessoa, andando normalmente, desenvolve uma velocidade média da ordem de 1m/s. Que distância, aproximadamente, essa pessoa percorrerá, andando durante 120 segundos? 

40) Um foguete é lançado à Lua com velocidade constante de 17500 km/h, gastando 22 horas na viagem. Calcule, com esses dados, a distância da Terra à Lua em quilômetros.