QUESTÃO 1 (Unicap - PE) Calcule o valor de x, a fim de que o determinante da matriz A seja nulo.
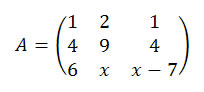
QUESTÃO 2 (U.F. Ouro Preto – MG) Considere a matriz:
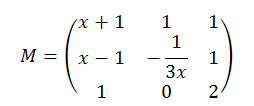
QUESTÃO 3 Determine o valor de x para que o determinante da matriz A seja igual a 8.
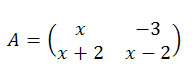
QUESTÃO 4 O determinante da matriz A é igual a -2. Se B e C são as matrizes obtidas, respectivamente, pela substituição em A do menor e do maior valor de y encontrados, calcule a matriz transposta do produto de B por C.
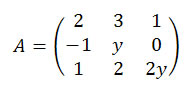
QUESTÃO 5 (Unicamp - SP) Seja a um número real e seja:
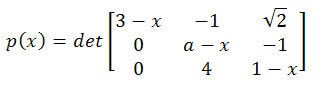
a) Para a=1, encontre todas as raízes da equação p(x)=0
b) Encontre os valores de a para os quais a equação p(x)=0 tem uma única raiz real.
GABARITO:
1) X = 13
2) -6x² + 7x -1
3) x = -2 ou x = 1
4) x = 0 ou x = -5/4
5) a) Façamos o determinante com o valor de a = 1:
.jpg)
Temos o produto de duas parcelas igual a zero, então teremos duas situações:
3 - x = 0 ou (1 - x) 2 + 4 = 0
Na primeira temos que x = 3; na segunda não é possível determinar uma solução.
Logo, temos apenas uma raiz possível quando a for igual a
b)
.jpg)
Novamente teremos duas situações: uma onde x=3 e a outra temos que determinar para quais valores de a teremos apenas a solução x = 3:
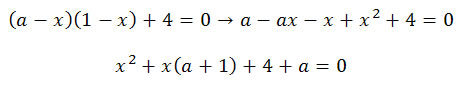
Para que só exista uma única raiz, essa equação do segundo grau não deve ter raiz, ou seja, seu discriminante deve ser menor que zero.

