4) No lançamento de dois dados perfeitos, qual a probabilidade de que a soma dos resultados obtidos seja igual a 6?
5) Considerando todos os divisores positivos do numeral 60, determine a probabilidade de escolhermos ao acaso, um número primo.
7) Em uma urna existem bolas enumeradas de 1 a 15. Qualquer uma delas possui a mesma chance de ser retirada. Determine a probabilidade de se retirar uma bola com número nas seguintes condições:
a) parb) primo
c) par ou primo
d) par e primo
8) Qual é a probabilidade de, no lançamento de 4 moedas, obtermos cara em todos os resultados?
a) 2%
b) 2,2%
c) 6,2%
e) 4%
f) 4,2%
9) Duas moedas e dois dados, todos diferentes entre si, foram lançados simultaneamente. Qual é o número de possibilidades de resultados para esse experimento?
a) 146
b) 142
c) 133
d) 144
e) 155
10) Qual é o número total de possibilidades de resultado no lançamento de 5 moedas?
a) 2
b) 5
c) 10
d) 24
e) 32
RESPOSTAS:
QUESTÃO 1.
Neste exercício o espaço amostral possui 12 elementos, que é o número total de bolas, portanto a probabilidade de ser retirada uma bola verde está na razão de 5 para 12.
Sendo S o espaço amostral e E o evento da retirada de uma bola verde, matematicamente podemos representar a resolução assim:
QUESTÃO 2
Através do princípio fundamental da contagem podemos determinar o número total de agrupamentos ao lançarmos três moedas.
Como cada moeda pode produzir dois resultados distintos, três moedas irão produzir 2 . 2 . 2 resultados distintos, ou seja, poderão produzir 8 resultados distintos. Este é o nosso espaço amostral.
Dentre as 8 possibilidades do espaço amostral, o evento que representa todas as moedas com a mesma face para cima possui apenas 2 possibilidades, ou tudo cara ou tudo coroa, então a probabilidade será dada por:
QUESTÃO 3
Sabemos que a probabilidade da mulher engravidar em um mês é de 20%, que na forma decimal é igual a 0,2. A probabilidade dela não conseguir engravidar é igual a 1 - 0,2, ou seja, é igual a 0,8.
Este exercício trata de eventos consecutivos e independentes (pelo menos enquanto ela não engravida), então a probabilidade de que todos eles ocorram, é dado pelo produto de todas as probabilidades individuais. Como a mulher só deve engravidar no quarto mês, então a probabilidade dos três meses anteriores deve ser igual à probabilidade dela não engravidar no mês, logo:
0,1024 multiplicado por 100% é igual a 10,24%.
Então:
QUESTÃO 4
Para que a soma seja 6, precisamos das seguintes faces: {(1,5), (2,4), (3,3), (4,2), (5,1)}. E considerando que o espaço amostral do lançamento de dois dados e representado pela multiplicação 6 * 6 = 36, temos a seguinte probabilidade:
A probabilidade é de 5/36, aproximadamente 13,88% de chance.
QUESTÃO 5
Divisores de 60: (1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60). Temos um espaço amostral de 12 elementos, dos quais 3 são primos. Portanto, a probabilidade de escolhermos ao acaso, um número primo dentro dos divisores do número 60, será dada por:
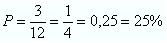
A probabilidade é de 25% de chance.
QUESTÃO 6
A probabilidade de escolhermos 1 dentre 2 travessas é igual 1/2.
A probabilidade de escolhermos um pastel na primeira travessa é 3 em 8, ou seja, é 3/8 e como a probabilidade de escolhermos a primeira travessa é 1/2, temos:
A probabilidade de escolhermos um pastel na segunda travessa é 4 em 6, isto é 4/6 e como a probabilidade de escolhermos a segunda travessa é igual a 1/2, temos:
Então a probabilidade de escolhermos um pastel é igual a:
QUESTÃO 7
Espaço amostral: (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15)
a) No espaço amostral de 15 números, temos 7 números pares.
P = 7/15 = 0,466 = 46,6%
b) Temos 6 números primos dentre o espaço amostral de 15 números.
P = 6/15 = 0,4 = 40%
c)
Número par = 7 possibilidades entre 15
Número primo = 6 possibilidades entre 15
Par ∩ primo = 1
P(par) + P(primo) – P (par ∩ primo)
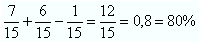
d) Dentro do intervalo dado, temos um único número que satisfaz a condição de ser par e primo ao mesmo tempo, que é o número 2. Portanto, temos a seguinte probabilidade:
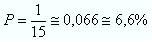
QUESTÃO 8
Primeiramente, é necessário encontrar o número total de possibilidades de resultados:
2·2·2·2 = 16
Posteriormente, devemos encontrar o número de possibilidades de obter cara em todos os resultados. Na realidade, só existe uma possibilidade de que isso aconteça.
Por fim, basta dividir o segundo pelo primeiro:
1 = 0,0625
16
Multiplicando 6,25 por 100, para obter um percentual, teremos: 6,25%
Gabarito: Letra C.
QUESTÃO 9
Para calcular o número de possibilidades de resultados de um experimento nesses moldes, multiplique o número de resultados possíveis de cada objeto em observação. No caso de cada moeda, 2 resultados, e de cada dado, 6 resultados:
2·2·6·6 = 4·36 = 144
Gabarito: Letra D.
QUESTÃO 10
O número total de resultados que pode ser obtido no lançamento de duas moedas é encontrado multiplicando-se a quantidade de resultados da primeira moeda pela quantidade da segunda e assim por diante. Observe:
2·2·2·2·2 = 32
Portanto, são 32 possibilidades diferentes.
Gabarito: Letra E.