TRIGONOMETRIA NO TRIÂNGULO RETANGULO - PARTE I - 9º ANO

 01) Calcule o seno, o cosseno e a tangente dos ângulos agudos assinalados nos triângulos a seguir:

02) Um topógrafo instala um teodolito a uma altura de 1,7 metros do solo e observa o topo de um prédio sob um ângulo de 40º. Estando o teodolito e o prédio em um mesmo terreno plano e distante um do outro 80 metros, determine a altura do prédio, aproximadamente. Dado tan 40º = 0,84.

03) Na praia foi medido a distância entre dois pontos distintos A e B conforme mostra a figura. A distância de A até B é 750 metros e de A até P é 620 metros, além do ângulo B de 60º. 

Encontre a distância, em metros, da ilha até a praia (aproximadamente).

04) Um topógrafo foi chamado para obterá altura de um edifício. Para fazer isto, ele colocou um teodolito (instrumento para medir ângulos) a 200m do edifício e mediu um ângulo de 30º, como indicado na figura abaixo. Sabendo que o teodolito está a 1,5 m do solo, encontre a altura do edifício.

05)  O ângulo de elevação do pé de uma árvores, a 50m da base de uma encosta, ao topo a encosta é de 60º. Que medida deve ter um cabo para ligar o pé da árvore ao topo da encosta?

06)  Do alto da torre de uma plataforma marítima de petróleo, de 45 m de altura, o ângulo de depressão em relação à proa de um barco é de 60º. A que distância o barco está da plataforma?

07)Uma torre tem 20 m de altura e uma pomba voou em linha reta do seu topo até o ponto M. A distância do centro da base do monumento até o ponto M é igual a 15m, como mostra a ilustração abaixo

Qual é a  distância percorrida por essa pomba, em metros?

08) Duas ruas de uma cidade mineira encontram-se em P formando um ângulo de30º. Na rua Rita, existe um posto de gasolina G que dista 2 400 m de P, conforme mostra a ilustração abaixo Sabendo que cos 30º 0,86, sen 30º 0,50 e tg 30º 0,68, a distância d, em metros, do posto G à Rua Reila é aproximadamente igual a

A) 1 200                 B) 1 392                      C) 2 064            D) 2 79                         E) 4 800 

09) Um helicóptero para sobrevoar m região, parte do ponto A do solo e sobe verticalmente 250m; em seguida voa horizontalmente 160m; para o leste; finalmente, desce verticalmente 130m ate o ponto B. Nessas condições, a distância entre os pontos A e B é, em metros. 

10) Para permitir o aceso a um monumento que está em um pedestal de 2m de altura, vai ser construída uma rampa com inclinação de 30 com o solo, conforme a ilustração. 

Qual é o comprimento da rampa ?

11) Gustavo encostou uma escada numa parede de sua casa de tal modo que o topo da escada ficou a uma altura de 3m em relação ao chão. Considerando que a escada forma um ângulo de 30º com a parede, calcule o comprimento da escada. 

(Dados: sen 30º =1/2; cos 30º =√3/2 e tg 30º =√3/3). Use: √3 = 1,7.

12) Um avião levanta vôo sob um ângulo de 30º em relação á pista. Qual será a altura do avião quando percorrer 4000m em linha reta?

13 - Determine os valores de x, y, w e z em cada caso:

14 - (Cesgranrio) Uma rampa plana, de 36 m de comprimento, faz ângulo de 30° com o plano horizontal. Uma pessoa que sobe a rampa inteira eleva-se verticalmente de:

a) 6√3 m.                b) 12 m.       c) 13,6 m.             d) 9√3 m.    e) 18 m.

15 - No triângulo retângulo da figura abaixo, determine as medidas de x e y indicadas (Use: sen 65° = 0,91; cos 65° = 0,42 ; tg 65° = 2,14)

 

17 ) Considerando o triângulo retângulo ABC da figura, determine as medidas a e b indicadas. (Sen 60° = 0,866)

18 ) Sabe-se que, em um triângulo retângulo isósceles, cada lado congruente mede 30 cm. Determine a medida da hipotenusa desse triângulo.

Nos triângulos das figuras abaixo, calcule tg Â, tg Ê, tg Ô:

a) 

b)       
c) 

19 ) Sabendo que o triângulo retângulo da figura abaixo é isósceles, quais são os valores de tg  e tg Ê?

20 – (Cesgranrio) – Uma rampa plana, de 36 m de comprimento, faz ângulo de 30° com o plano horizontal. Uma pessoa que sobe a rampa inteira eleva-se verticalmente de:

a) 6√3 m.                       b) 12 m.                      c) 13,6 m.                 d) 9√3 m.             e) 18 m.

21 - As alturas (em relação ao nível do mar) em que estão dois pontos A e B são, respectivamente, 812m e 1020m. Do ponto A vê-se o ponto B sob um ângulo de 30° com o plano horizontal, conforme a figura.

Determinar a distância entre os pontos A e B.

a) 416 metros   b) 350 metros   c) 400 metros   d) 250 metros   e) 500 metros

22 - Quando o Sol está a 30° acima do horizonte, um edifício de 100 metros projeta uma sombra de quantos metros?

a) 172,2 metros   b) 173,2 metros   c) 273,2 metros   d) 173,8 metros   e) 133,2 metros

23 -A quantos graus acima do horizonte deve estar o Sol para que um edifício projete uma sombra com o seu tamanho?

a) 35º                    b) 40º                   c) 65º                       d) 45º                          e) 55º

24- Do lugar onde me encontro, avisto uma torre segundo um ângulo de 32° com a horizontal.Se me aproximo 25 metros da torre, o ângulo é de 50°.

Qual é a altura da torre?

a) 22,84 metros.   b) 32,84 metros.   c) 42,84 metros.   d) 52,84 metros.  e) 62,84 metros.

25 - Uma escada de 3 metros está apoiada em uma parede. Se o pé da escada está apoiado no chão a uma distância de 1,2 m da parede, qual a medida aproximada do ângulo que a escada forma com o chão?

26 - Um paraquedista salta de um avião quando este se encontra a 1.800 m de altura.

Devido à velocidade do avião e da ação do vento, o paraquedista salta do ponto P$P$, mas cai no ponto A$A$, conforme indica a figura.
A que distância do ponto B o paraquedista vai cair?

27 - A figura abaixo representa um avião que decolou sob um ângulo constante de 40º e percorreu em linha reta 8000 m. Nesta situação, qual a altura que se encontrava o avião ao percorrer essa distância?

Considere:

sen 40º = 0,64
cos 40º = 0,77
tg 40º = 0,84

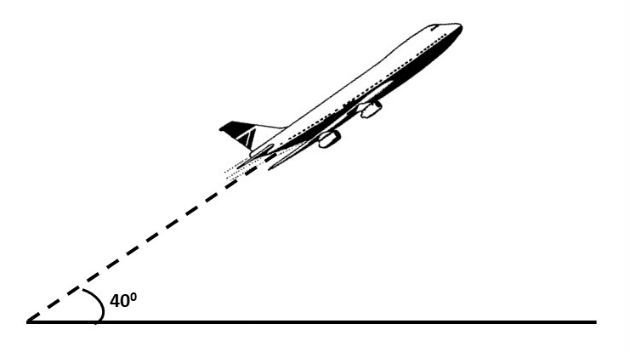
a) 4284 metros.   b) 5284 metros.   c) 4284 metros.   d) 5284 metros.   e) 5120 metros.

28 - Um menino avista o ponto mais alto de um morro, conforme figura abaixo. Considerando que ele está a uma distância de 500 m da base do morro, calcule a altura (h) deste ponto.

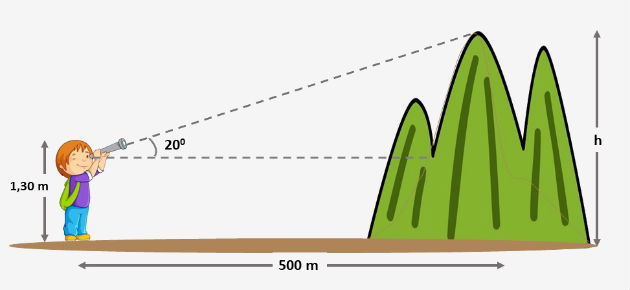
Considere:

sen 20º = 0,34
cos 20º = 0,93
tg 20º = 0,36

a) 281,3 m        b) 183,3 m.             c) 481,3 m.           d) 181,3 m.                e) 180,3 m.

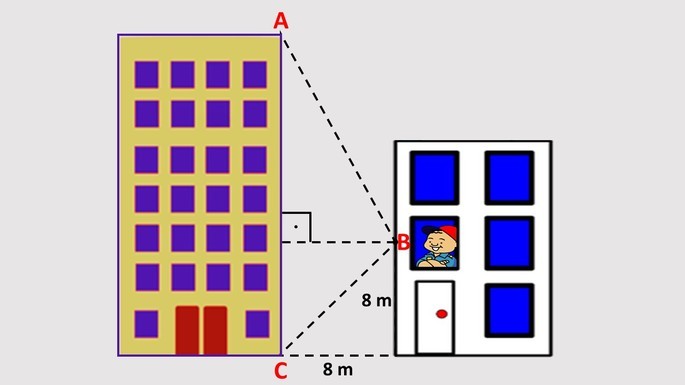
29 - Pedro, localizado a 8 metros do chão, está observando o prédio vizinho. Sabendo que a sua distância para o prédio vizinho é de 8 m e entre as duas estruturas forma-se um triângulo, cujo ângulo ABC é de 105º, determine a altura do prédio que Pedro está observando.

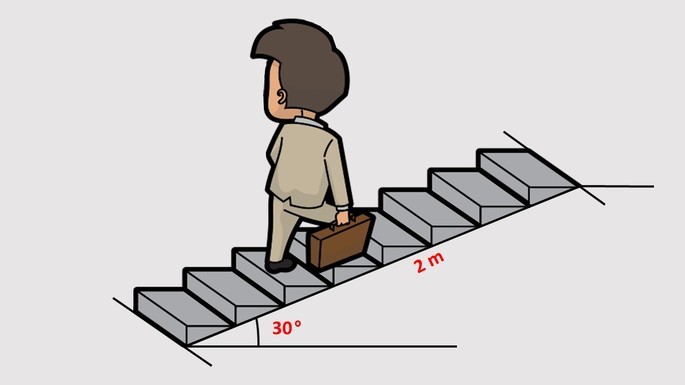
30 - João trabalha em um prédio e todos os dias tem que subir uma escada de 8 degraus, que tem aproximadamente 2 metros de comprimento e 30 graus de inclinação. De acordo com a figura a seguir, determine a altura de cada degrau.