a) 10 b) 12. c) 15. d) 18
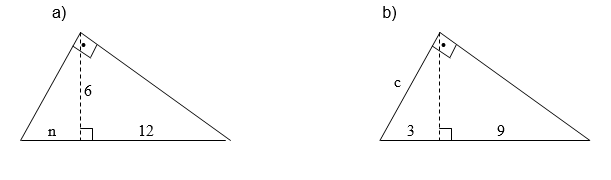
2) Aplicando as relações métricas nos triângulos retângulos abaixo, determine o valor da incógnita:
3)
Considere
a figura abaixo e determine:
a)
a
medida do lado m
b)
a
medida do lado n
c)
a
medida do lado p
d) o perímetro do trapézio ABCD

5- Considerando o triângulo abaixo, determine o valor da expressão x² + y² .
6) Encontre o valor de y em cada relação:
7) A soma dos números correspondentes às medidas a, b, c e h no triângulo da figura abaixo formam uma senha que abre o cofre do senhor Adamastor.
Qual
a senha que abre o cofre do Adamastor?
a) 124 b) 134 c) 174 d) 144 e) n.d.a
8) Utilizando o Teorema de Pitágoras, determine o valor de x nos triângulos retângulos:
9)
A figura mostra um edifício que tem
a) 12 m. b) 30 m. c) 15 m. d) 17 m. e) 20 m.
10) Determine as medidas a, h, m e n no triângulo retângulo ABC a seguir.
11) Determine os valores de
b, c e h no triângulo retângulo ABC abaixo.
12) Em um retângulo ABCD, tem-se AB = 8 cm e BC = 6 cm. Determine:
a) a medida da diagonal
b) a distância do ponto B
à diagonal
c) a medida da projeção
ortogonal do lado
13) Em um triângulo
retângulo ABC, a hipotenusa BC
14) O perímetro de um triângulo equilátero mede 15cm. Determine a medida da altura desse triângulo.
15) Uma escada medindo 4m tem uma de suas extremidades apoiada no topo de um muro, e a outra extremidade dista 2,4 m da base do muro. Determine a altura desse muro.
16) Num trapézio retângulo, as bases medem 16cm e 4cm, respectivamente. O maior lado não paralelo mede
13cm. Qual o perímetro do trapézio?
17) Determine a medida da diagonal de um quadrado que tem 15 cm de lado.
18) Determine a medida da hipotenusa e o perímetro do triângulo:
19) As extremidades de um fio de antena totalmente esticado estão presas no topo de um prédio e no topo de um poste, respectivamente, de 16m e 4m de altura. Considerando-se o terreno horizontal e sabendo-se que a distância entre o prédio e o poste é de 9m, o comprimento do fio, em metros, é
a) 12
b)
15 c)
20 d)
25
20) Na figura, o triângulo ABC é retângulo em Â. Sabendo-se que AD = 2, CD = 8 e BD = 5, a medida do lado BC é:
. a) 11
b) 12
c) 13 d) 14
21) Na figura abaixo, a distância da casa à estrada é
1,2km.
a) Qual é a menor distância da árvore à caixad’água?
b) Qual é a menor distância da casa à árvore?
c) Qual é a menor distância da casa à caixa d’água?
22) A chácara de ângela tem a forma de um triângulo
retângulo e as dimensões indicadas na figura. Qual a distância entre o portão e
o poço?
23) A figura representa a vista frontal de uma casa. Determine as medidas x, y e h das dimensões do telhado dessa casa:
24)
Em um triângulo retângulo, os catetos medem 7cm e 24 cm. Determine a medida da:
a) hipotenusa
b) altura relativa à hipotenusa.
25)
Em um mapa, as cidades A, B e C são os vértices de um triângulo retângulo e o
ângulo reto está em A. A estrada AB tem 80 km e a estrada BC tem 100 km. Um rio
impede a construção de uma estrada que ligue diretamente a cidade A com a
cidade C. Por esse motivo, projetou-se uma estrada saindo de A e perpendicular
à estrada BC, para que ela seja a mais curta possível. Qual será o comprimento
da estrada que será construída?
26) Em um triângulo retângulo ABC, AH é a altura relativa ao lado BC, o cateto AB mede 15 cm e o segmento HC mede 16 cm. Determine a medida x da hipotenusa do triângulo ABC.
27) Em um triângulo retângulo as projeções dos catetos sobre a hipotenusa medem 6 cm e 8 cm. Determine a altura relativa à hipotenusa desse triângulo.
2x + 3 e x – 4 e a hipotenusa, por 3x – 11. Qual é o perímetro desse triângulo?
a)
a medida da hipotenusa
b)
a medida do outro cateto
c)
a medida da altura relativa à hipotenusa.
31) O triângulo retângulo ABC ao lado é
retângulo
32) O valor de x, y e z no triângulo retângulo abaixo é:
33) Em um triângulo retângulo as
projeções dos catetos sobre a hipotenusa medem
34) A medida da altura relativa À hipotenusa
de um triângulo retângulo é
35) Determine
a medida das projeções em um triângulo retângulo cuja hipotenusa mede
36) Em um triângulo retângulo a altura
relativa à hipotenusa mede
37) As medidas dos catetos de um triângulo retângulo são ( x + 5) cm e ( x + 1) cm e a hipotenusa ( x + 9) cm. Determine o perímetro desse triângulo.
38) No
triângulo ABC retângulo em A, determine as medidas a, c, n e h. E determine a área e
perímetro do triângulo ABC.
39) No
triângulo ABC retângulo em A, determine as medidas c, n, h, e b. E determine a área e
perímetro do triângulo ABC.
40) Num triângulo retângulo, a hipotenusa mede
a) a medida da altura relativa à hipotenusa.
b) a medida dos segmentos que a altura determina sobre a hipotenusa.
c) a área desse triângulo.
d) O perímetro desse triângulo.
41) Em um triângulo retângulo a
altura relativa à hipotenusa mede
42.
Determine o valor da incógnita:
43) Para executar um serviço, o trabalhador
apoiou na laje de sua casa a escada de
A
base da escada, apoiada sobre um piso horizontal está afastada
44) A respeito dos elementos de um triângulo retângulo, assinale a alternativa correta.
a) Um triângulo retângulo é assim conhecido por possuir pelo menos dois lados iguais.
b) O triângulo retângulo é assim conhecido por possuir pelo menos um ângulo de 180°, também conhecido como ângulo reto.
c) A hipotenusa é definida como o maior lado de um triângulo qualquer.
d) A hipotenusa é definida como o lado que se opõe ao maior ângulo de um triângulo qualquer.
e) A hipotenusa é definida como o lado que se opõe ao ângulo reto de um triângulo retângulo.
45) Na figura tem-se que AB ≅ BC e F é ponto médio do lado BE do retângulo BCDE. Determine: a) a medida x indicada na figura. b) a área do retângulo BCDE.