1) (IFAL/2017) Determine o valor de k para que a equação x² + kx + 6 = 0 tendo como raízes os valores 2 e 3.
a) 5
b) 6
c) -6
d) -5
e) 0
2) (UNIFOR CE/2018) Júlia, aluna do curso de Biologia, está pesquisando o desenvolvimento de certo tipo de bactéria. Para a realização dessa pesquisa, ela utiliza um tipo de estufa para armazenar as bactérias.Sabe-se que dentro da estufa a temperatura em graus Celsius é dada pela equação T(h) = –h2 + 20h – 65 onde h representa as horas do dia. Júlia sabe também que o número de bactérias será o maior possível quando a estufa atinge sua temperatura máxima, e nesse exato momento ela deve tirar as bactérias da estufa.
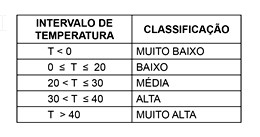
Baseado na tabela acima, podemos afirmar que a estudante obtém o maior número de bactérias, quando a temperatura no interior da estufa está classificada como
a) baixa.
b) muito baixa.
c) alta.
d) muito alta.
e) média.
3) (IFBA/2017) Durante as competições Olímpicas, um jogador de basquete lançou a bola para o alto em direção à cesta. A trajetória descrita pela bola pode ser representada por uma curva chamada parábola, que pode ser representada pela expressão:
h = –2x2 + 8x
(onde “h” é a altura da bola e “x” é a distância percorrida pela bola, ambas em metros)
(onde “h” é a altura da bola e “x” é a distância percorrida pela bola, ambas em metros)
A partir dessas informações, encontre o valor da altura máxima alcançada pela bola:
a) 4 m
b) 10 m
c) 6 m
d) 8 m
e) 12 m
4) (UNISC RS/2015) A soma de todas as raízes da equação: (2x² + 6x – 20).(5x – 1) = 0 é
a) 14/5
b) 4/5
c) -14/5
d) 16/5
e) -16/5
5) (IFSC/2017) Pedro é pecuarista e, com o aumento da criação, ele terá que fazer um novo cercado para acomodar seus animais. Sabendo-se que ele terá que utilizar 5 voltas de arame farpado e que o cercado tem forma retangular cujas dimensões são as raízes da equação x² – 45x + 500 = 0, qual a quantidade mínima de arame que Pedro terá que comprar para fazer esse cercado?
Assinale a alternativa CORRETA.
a) 450 m.
b) 500 m.
c) 200 m.
d) 225 m.
e) 545 m.
6) (IFMA/2016) As raízes da equação v² + 8v + k = 0 são os números v1 e v2, onde k é uma constante real. Se v1 -3v2 , o valor da constante k é:
a) 15
b) 12
c) -7
d) 10
e) -15
7) (UNIFAP AP/2015) Ainda estudando sobre equações do segundo grau. Tentam resolver o seguinte problema. O produto de dois números é igual a –128 e a soma destes números dividido por 4 é igual a 7, quais são esses números.
Qual é a alternativa que eles devem marcar como correta:
a) –4 e 32
b) 4 e –32
c) 8 e –16
d) –2 e 64
e) 1 e –128
8) (UDESC SC/2018) A regra para encontrar dois números cuja soma e cujo produto são dados, era enunciada pelos babilônios como “Eleve ao quadrado a metade da soma subtraia o produto e extraia a raiz quadrada da diferença. Some ao resultado a metade da soma. Isso dará o maior dos números procurados. Subtraia-o da soma para obter o outro número.” (LIMA, Elon Lages. Números e Funções Reais. SBM, 2013. Coleção PROFMAT. p.108.)
Atualmente a fórmula que dá a resposta para esse problema é conhecida como:
a) Teorema de Pitágoras
b) Média aritmética
c) Média geométrica
d) Fórmula de Bháskara
e) Regra de três composta.
9) (IFSC/2017) Dada a equação quadrática 3x2 + 9x – 120 = 0, determine suas raízes.
Assinale a alternativa que contém a resposta CORRETA.
a) –16 e 10
b) -8 e 5
c) –5 e 8
d) –9 e 15
e) -10 e 16
10) (IFAL/2017) Determine o valor de k na equação
x² – 12x + k = 0, de modo que uma raiz seja o dobro da outra:
a) 28
b) 24
c) 18
d) 12
e) 32
GABARITO:
1) D
2) C
3) D
4) C
5) A
6) A
7) A
8) D
9) B
10) E