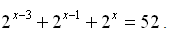1)
2) Determine
o conjunto solução da seguinte equação exponencial:
3) (Uneb-BA) A expressão P(t) = K · 20,05t fornece o número P de milhares de habitantes de uma cidade, em função do tempo t, em anos. Se, em 1990, essa cidade tinha 300.000 habitantes, quantos habitantes, aproximadamente, espera-se que ela tenha no ano 2000?
A) 352.000
B) 401.000
C) 423.000
D) 439.000
E) 441 000
4) Descubra
o valor de x para que a igualdade abaixo seja válida.
log2 (3x
+ 10) – log2 x = log2 5
5) Resolva a equação logarítmica logx +
3 (5x – 1) = 1.
6) Resolva a equação log2 (x
- 1) + log2 (x - 2) = 1
7) (UP).
A solução da equação logarítmica log10 (x-4) = 2 é:
A) x = 6.
B) x = 10.
C) x = 50.
D) x = 100.
E) x = 104.
8) Resolva
a equação: log3 ( 2x - 1) = 4
9) Resolva
a equação logarítmica abaixo, determinando o valor de x:
log10 (4x
– 2) = log10 2 – log10 (2x – 1)
10) Dada
a função f(x) = 2x+3 + 10, o valor de x para que f(x) = 42 é
de:
A) 2
B) 3
C) 4
D) 5
E) 6