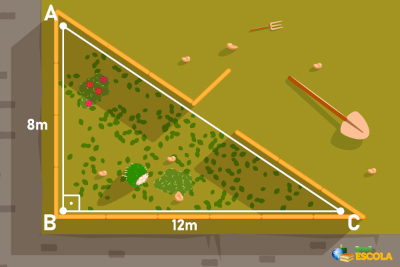
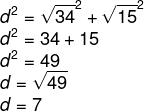1 - Um terreno retangular será dividido ao meio, pela sua diagonal, formando dois triângulos retângulos. A metade desse terreno será cercada com 4 fios de arame farpado. Sabendo que as dimensões desse terreno são de 20 metros de largura e 21 metros de comprimento, qual será a metragem mínima gasta de arame?
A) 300 metros
B) 280 metros
C) 140 metros
D) 70 metros
E) 29 metros
2 - A área do triângulo retângulo que possui base medindo 5 cm e hipotenusa medindo 13 cm é igual a:
A) 30 cm²
B) 60 cm²
C) 24 cm²
D) 16 cm²
E) 12 cm²
3 - Uma represa no formato retangular possui dimensões de 30 metros por 40 metros. Qual será a distância percorrida por uma pessoa que atravessa essa represa pela sua diagonal?
A) 45 metros
B) 50 metros
C) 65 metros
D) 70 metros
E) 80 metros
4 - (Fundatec) O famoso teorema de Pitágoras nos permite calcular o valor da hipotenusa e dos catetos formadores do triângulo retângulo. Sabendo que a hipotenusa de um determinado triângulo mede 10 cm e o cateto oposto mede 6 cm, assinale a alternativa que contém a medida do cateto adjacente:
A) 7
B) 8
C) 9
D) 10
E) 11
5 - (IFG 2019) Considere que o tamanho de uma televisão, dado em polegadas, corresponde ao comprimento da sua diagonal e que, no caso de televisores de tamanho normal, a largura e a altura seguem, ordenadamente, a relação 4:3. Observe a figura abaixo e considere 1 polegada = 2,5 cm.

Com relação a uma televisão plana de 40 polegadas, é correto afirmar que sua largura e sua altura são, respectivamente:
A) 60 cm e 45 cm
B) 80 cm e 60 cm
C) 64 cm e 48 cm
D) 68 cm e 51 cm
6 - (IBEG) Um empresário adquiriu um terreno comercial em formato triangular. As medidas perpendiculares são de 120 metros e 160 metros. Após a limpeza do terreno, o proprietário decidiu construir uma cerca de arame liso com 8 fios em volta de todo o perímetro do terreno. Cada metro do fio de arame custa R$ 1,50. Diante das informações apresentadas, calcule o perímetro total do terreno utilizando o teorema de Pitágoras, a quantidade de metros de arames a ser utilizado e o valor do custo com a aquisição dos fios de arame.
A) Perímetro total de 280 metros; 2.240 metros de fios; custo de R$ 3.360.
B) Perímetro total de 300 metros; 2.400 metros de fios; custo de R$ 3.600.
C) Perímetro total de 350 metros; 2.800 metros de fios; custo de R$ 4.200.
D) Perímetro total de 480 metros; 3.840 metros de fios; custo de R$ 5.760.
E) Perímetro total de 400 metros; 3.200 metros de fios; custo de R$ 4.800.
7 - (IFG 2020) O desmatamento tem sido uma problemática crescente no Brasil. Supondo que, ao efetuar o desmatamento de uma determinada área, um madeireiro se depara com uma árvore que já se encontra quebrada; parte do tronco da árvore que se manteve fixa ao solo mede 3 m e forma com este um ângulo de 90⁰; a ponta da parte quebrada que toca o solo encontra-se a 4 m de distância da base da árvore. Qual era a altura da árvore antes de se quebrar:
A) 5 m
B) 7 m
C) 8 m
D) 9 m
8 - Um carro se desloca por uma rampa inclinada. Essa rampa possui 60 metros de comprimento e altura máxima de 10 metros, conforme a imagem:

A distância x entre o ponto A e B é de aproximadamente:
A) 45 metros
B) 50 metros
C) 55 metros
D) 58 metros
E) 59 metros
9 - Em seu quintal, Sara decidiu criar um jardim no formato de um triângulo retângulo. Para isso é importante que ela saiba as dimensões dos lados desse triângulo. Analisando a imagem, podemos afirmar que o valor da hipotenusa é: (Use √13 = 3,6)
A) 10 cm
B) 13,4 cm
C) 15,2 cm
D) 16 cm
E) 14,4 cm
10 - Analisando os triângulos a seguir, podemos afirmar que a soma x + y é igual a:
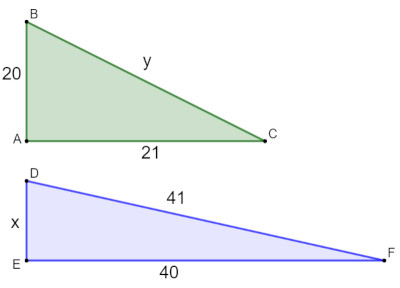
A) 29
B) 9
C) 30
D) 38
E) 40
11 - Ao encerrar o expediente de trabalho, Sunara chamou um táxi para retornar à sua casa. No caminho, o semáforo sinalizou a cor amarela, mas o motorista ainda estava muito distante. Em seguida, foi sinalizado vermelho, e o motorista parou a uma distância horizontal de 3 m de um semáforo que possui 4 m de altura. Analisando a imagem, qual é o comprimento representado por x:
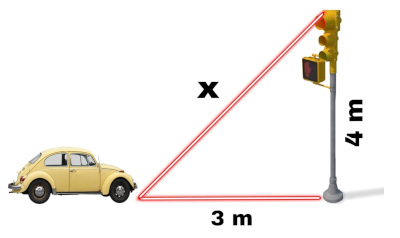
A) 2 m
B) 3 m
C) 4 m
D) 5 m
E) 6 m
12 - Utilize a relação pitagórica para encontrar a diagonal.
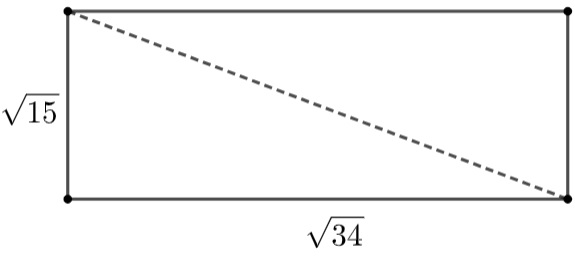
A) 5
B) 6
C) 7
D) 42
E) 49
GABARITO:
1 - Alternativa B
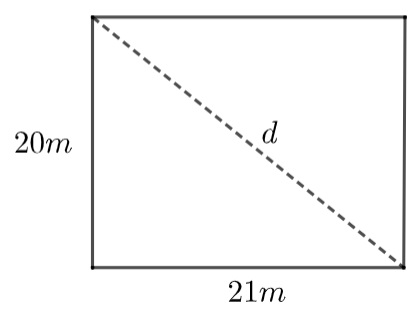
Para encontrar a hipotenusa, que é diagonal d desse retângulo, aplicamos o teorema de Pitágoras.
d² = 20² + 21²
d² = 400 + 441
d² = 841
d = √841
d = 29
Sabendo que as dimensões do triângulo são 20, 21 e 29, vamos calcular seu perímetro.
P = 20 + 21 + 29 = 70 metros
Como haverá 4 fios de arame farpado, multiplicando o perímetro por 4, encontraremos a metragem de arame necessária.
70 × 4 = 280 metros
2 - Alternativa A
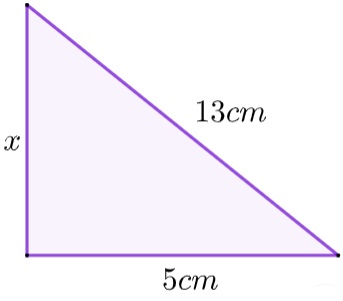
Como o triângulo é retângulo, seja x a sua altura, que coincide com o cateto que não conhecemos, aplicando o teorema de Pitágoras, temos que:
x² + 5² = 13²
x² + 25 = 169
x² = 169 – 25
x² = 144
x = √144
x = 12
Para calcular a área do triângulo, temos que:
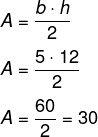
3 - Alternativa B
Desenhando a situação, temos que:
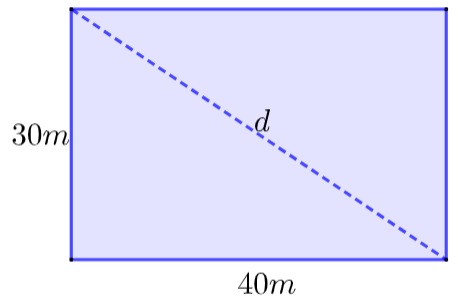
Pelo teorema de Pitágoras, temos que:
d² = 30² + 40²
d² = 900 + 1600
d² = 2500
d = √2500
d = 50 metros
4 - Alternativa B
Aplicando o teorema de Pitágoras, temos que:
10² = 6² + x²
100 = 36 + x²
100 – 36 = x²
64 = x²
x = √64
x = 8
5 - Alternativa B
Sabendo que a TV tem dimensões proporcionais a 3 e 4, seja 3k e 4k o comprimento e a altura respectivamente, temos que:
40² = (3k)² + (4k)²
1600 = 9k² + 16k²
1600 = 25k²
1600/25 = k²
64 = k²
k = √64
k = 8
Sabendo que k = 8, então as dimensões da TV em polegadas são:
4k → 4 × 8 = 32
3k → 4 × 3 = 24
Para transformar em centímetros, basta multiplicar por 2,5, já que uma polegada equivale a 2,5 cm.
32 × 2,5 = 80 cm
24 × 2,5 = 60 cm
6 - Alternativa D
Primeiro encontraremos a hipotenusa x.
x² = 120 ² + 160²
x² = 14.400 + 25.600
x² = 40.000
x = √40.000
x = 200
Agora calculando o perímetro, temos que:
200 + 120 + 160 = 480 metros
Como serão dadas 8 voltas, então:
480 × 8 = 3840
Sabendo que o metro custa R$1,50, então:
1,50 × 3.840 = 5760,00
7 - Alternativa C
Para encontrar o valor da parte da árvore que quebrou, basta aplicar o teorema de Pitágoras.
x² = 3² + 4²
x² = 9 + 16
x² = 25
x = √25
x = 5
Como ainda há 3 metros que ficaram fixos no solo, a altura da árvore é de 5 + 3 = 8 metros.
8 - plicando o teorema de Pitágoras, temos que:
60² = 10² + x²
3600 = 100 + x²
3600 – 100 = x²
x² = 3500
x = √3500
x = 59,16 metros
9 - Alternativa E
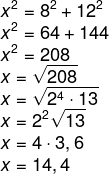
10 - Alternativa D
Encontrando o valor de x, temos que:
41² = x² + 40²
1681 = x² + 1600
x² = 1681 – 1600
x² = 81
x = √81
x = 9
Encontrando o valor de y:
y² = 21² + 20²
y² = 441 + 400
y² = 841
y = √841
y = 29
x + y = 9 + 29 = 38
11 - Sabemos que:
x² = 3² + 4²
x² = 9 + 16
x² = 25
x = √25
x = 5
12 - Alternativa C
Aplicando o teorema de Pitágoras, temos que: